import numpy as np
def frac_one(n: int, i: int = 0):
i += 1
n -= 1
nominator = 1 + 2 * i
if n == 0:
return 1
else:
return 2 + (1 + 2 * i) ** 2 / frac_one(n, i)
def frac_inf(n: int, i: int = 0):
i += 1
n -= 1
nominator = 1 + 2 * i
if n == 0:
return np.inf
else:
return 2 + (1 + 2 * i) ** 2 / frac_inf(n, i)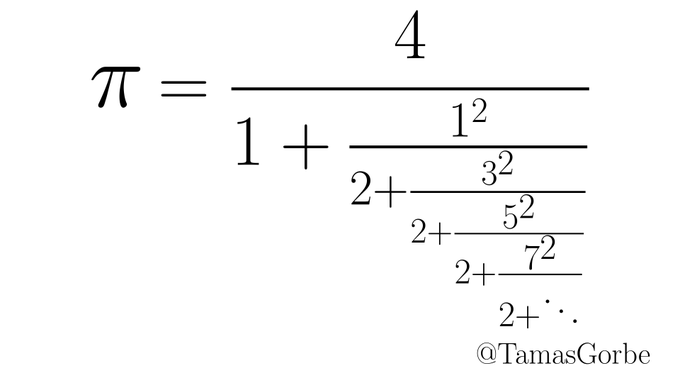
\(\pi = \frac{4}{1+\frac{1^2}{2 + recursion(n)}}\)
def pi_approx(func, n_iters):
return 4 / (1 + 1 / func(n_iters))def pi_mixed(n_iters):
a = pi_approx(frac_one, n_iters)
b = pi_approx(frac_inf, n_iters)
return (a + b) / 2# let's use our laptop's recursion limit to get maximum accuracy
import sys
max_recursion = int(sys.getrecursionlimit() * 0.98)
max_recursion2940pi_approx(frac_one, max_recursion)3.141932789654053pi_approx(frac_inf, max_recursion)3.141252517545209print(
f"""
At recursion depth of {max_recursion} the approximation error is:
* {(np.pi - pi_approx(frac_one, max_recursion))/np.pi:.3%} for frac_one
* {(np.pi - pi_approx(frac_inf, max_recursion))/np.pi:.3%} for frac_inf
* {(np.pi - pi_mixed(max_recursion))/np.pi:.12%} for pi_mixed
"""
)
At recursion depth of 2940 the approximation error is:
* -0.011% for frac_one
* 0.011% for frac_inf
* -0.000000000313% for pi_mixed